
Sheldon Logan
and
Wyatt Toolson
Department of Mathematics
Harvey Mudd College
Particle Model Simulations of Locust Swarms
Sheldon Logan and Wyatt Toolson
Sheldon Logan and Wyatt Toolson
Harvey Mudd College Mathematics
Summer 2005

Sheldon Logan (HMC '06) is on the left.
He is an Engineering Major.
E-mail: slogan@hmc.edu
Wyatt Toolson (HMC '07) is on the right.
He is majoring in Mathematical Biology.
E-mail: wtoolson@hmc.edu
Particle Model Simulations of Locust Swarms
Locust swarms are social aggregations consisting of large numbers of individuals (on the order of 107-109) that cohesively travel great distances over an extended period of time. Often observed in northern Africa, these swarms tend to follow a basic pattern; locusts at the front of the swarm land and rest on the ground until overtaken by the back of the swarm, at which point they take off and make their way to the front of the swarm. When viewed from the side it resembles a wheel rolling along [1-4].
Previous research attempts have been made using traveling bands along with density gradients [5]. Our model relies on the attraction-repulsion forces exerted on an individual by the others in the swarm. Basic assumptions included a strong desire to maintain group cohesion while short-range repulsion kept individuals from running into each other. To meet these requirements, we assume that the velocity is the sum of the contributions of all other locusts in the swarm; these contributions scale like a Morse potential [6]:
where x is the inner-locust distances.
In Figure 1 we see a swarm suspended in mid air. Upon examination of the F, L parameter space, we observed that a small portion of parameter space, namely where FL3 < 1, held the necessary condition that as N increased, the swarm density remained roughly constant. Figure 1 shows the lattice structure that is maintained when operating in this space.
Figure 2 is a swarm that has settled onto the ground after the addition of gravity. When taking values from the above mentioned section of parameter space, a small increase in spacing between the row of locusts on the ground and the row right above them is observed. This effect is more greatly noted when using values of F and L not from this space, as seen in Figure 3.
Figure 4 is a movie of a rolling swarm with values of F and L coming from the desired section. Unfortunately, these numbers do not lead to the desired behavior that is observed in real life. Many locusts are left behind and the swarm appears to be smearing out as opposed to rolling.
Figure 5 is another movie with values coming from outside of the calculated space. Here we see that the swarm rolls quite well and follows the general observed behavior. However, the part of the swarm in the air still remains circular, even with the addition of noise.
Overall, we were encouraged with the results of our study. We were able to achieve a rolling swarm, which was the ultimate goal. However, the swarm that rolls properly will become more dense as N increases. During further study, we plan to look at ways to have the swarm roll as it should, but also increase in size as N grows larger.
This research was conducted partially at Harvey Mudd College and partially at UCLA under the guidance of Prof. Chad Topaz and Prof. Andrew Bernoff. We wish to thank the Howard Hughes Medical Institute and the National Science Foundation for financial support and Prof. Andrea Bertozzi for sponsoring this summer research opportunity.
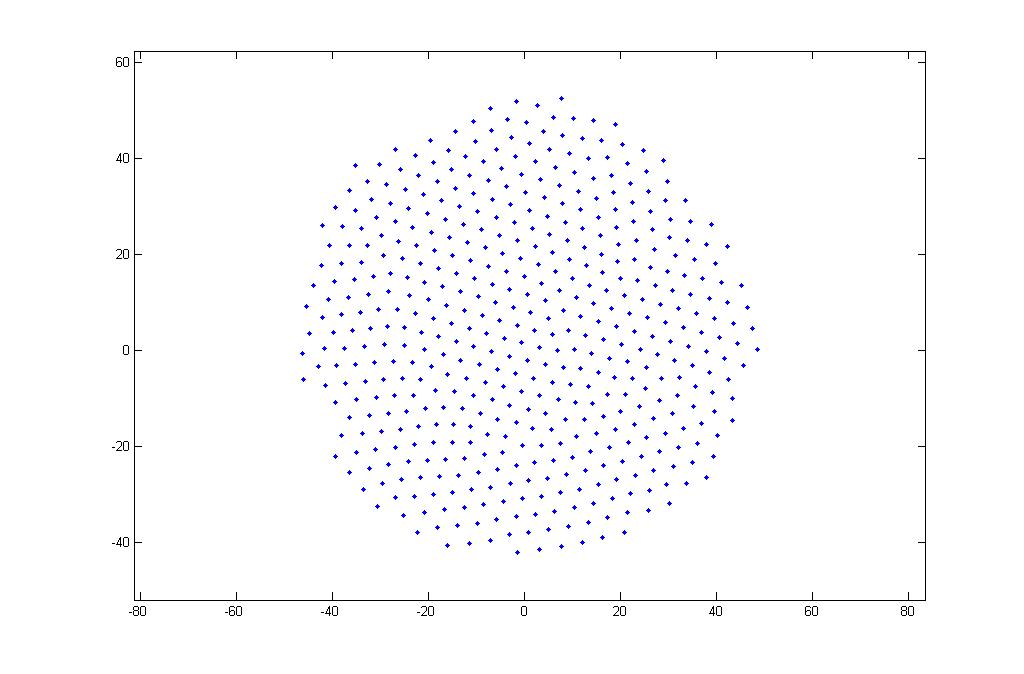
Figure 1: Swarm of locusts suspended in air.
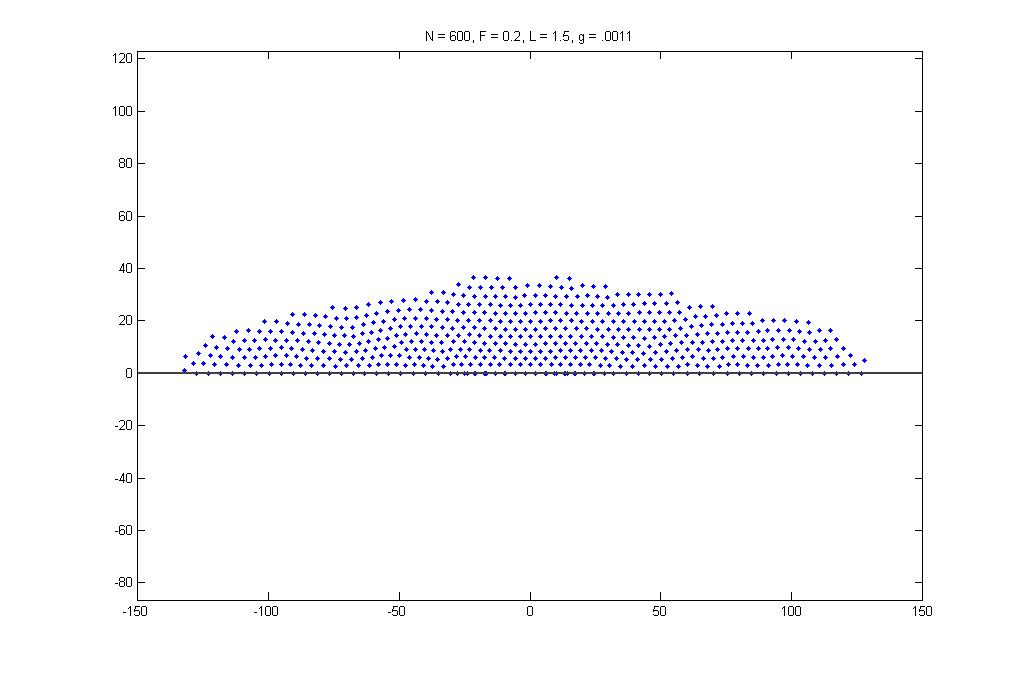
Figure 2: Locust swarm settled on ground with parameters from crystaline space.
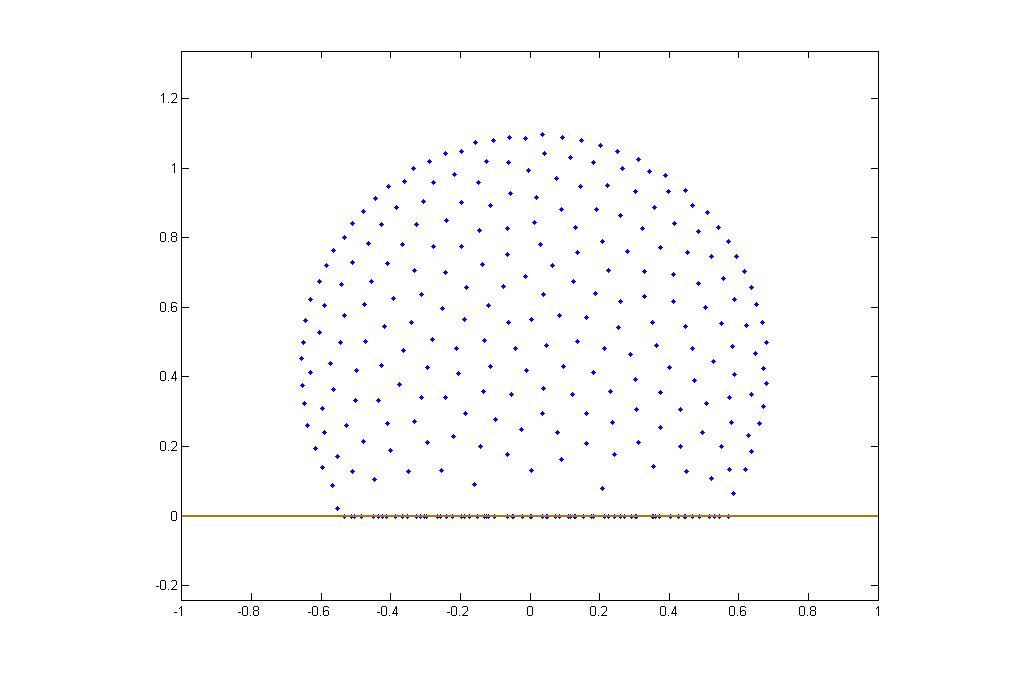
Figure 3: Locust swarm settled on ground wtih parameters from outside crystalline space.
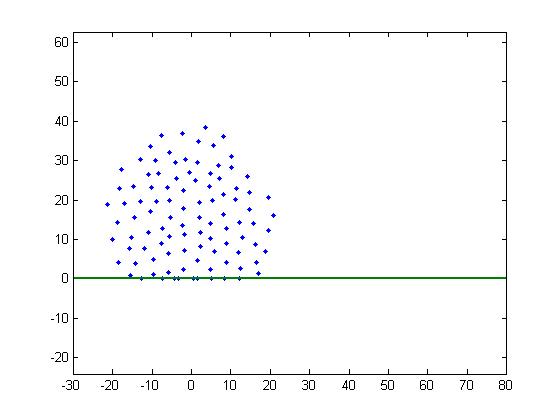
Figure 4: Movie of rolling swarm with parameters from within crystalline space.
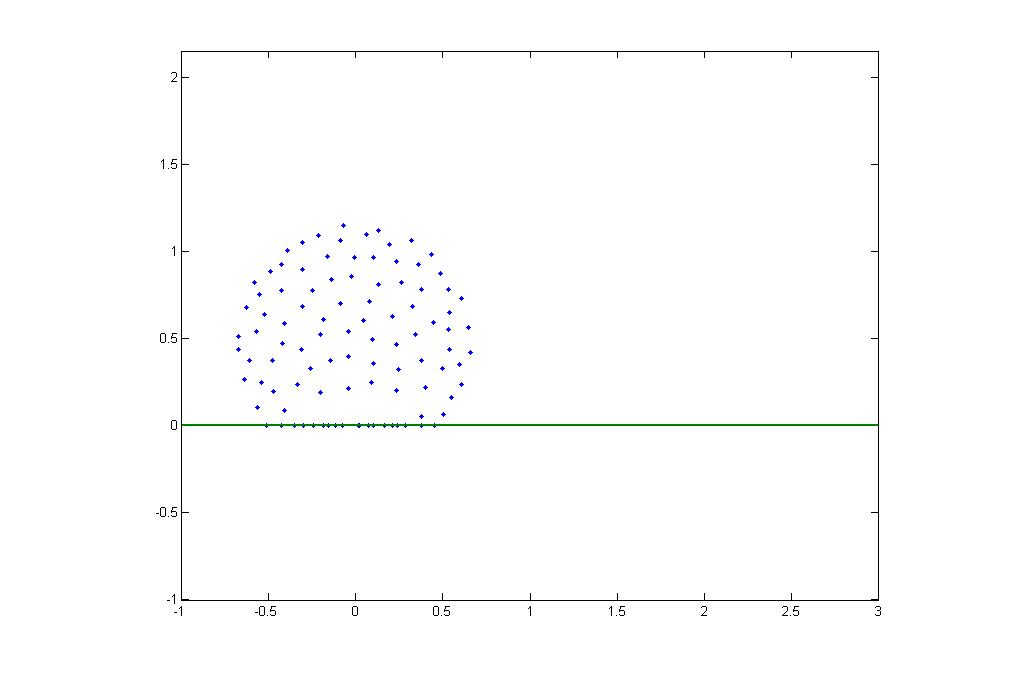
Figure 5: Movie of rolling swarm with parameters from outside crystalline space. High quality version.
References
- Albrecht, Frederic O. Polymorphisme Phasaire et Biologie des Acridiens Migratuers,Masson & Cie, Paris 1967.
- Uvarov, Boris P. Locusts and Grasshoppers.,The Imperial Bureau of Entomology, London 1928.
- Uvarov, Boris P. Grasshoppers and Locusts, Vol. I. University Press, Cambridge 1966.
- Uvarov, Boris P. Grasshoppers and Locusts, Vol. II. University Press, Cambridge 1977.
- Edelstein-Keshet, Leah; Watmough, James and Grunbaum, Daniel. Do travelling band solutions describe cohesive swarms? An investigation for migartory locusts, J. of Mathematical Biology, 36: 515-549, 1998.
- Saffre, F. and Deneubourg, J. L. Swarming Strategies for Cooperative Species, J. of Theoretical Biology, 214: 441-451, 2002.
- Mogilner, Alexander and Edelstein-Keshet, Leah. A non-local model for a swarm, J. of Mathematical Biology, 38: 534-570, 1999.
- Mogilner, A.; Edelstein-Keshet, L.; Bent, L and Spiros, A. Mutual interactions, potentials, and individual distance in a social aggregation, J. of Mathematical Biology, 47: 353-389, 2003.